Knots, Hopf Fibration and Hopfions

The hidden side of quipu knots?

Here are some additional thoughts on knots we discussed in the documentary about Quipu here -

The knot you see on the first image is also known as the Sailor's breastplate and is a knot used for joining two lines. It is particularly appropriate for very heavy rope or cable that is too large and stiff to be easily formed into other common bends. It will not jam even after carrying a significant load or being soaked with water.

What’s interesting is that there is a specific mathematical link called L8a8 that, when visualized and manipulated under certain conditions, resembles the seized carrick bend knot commonly used in practical settings. 

Links in mathematics are collections of knots that can be intertwined but do not intersect. They exist in three-dimensional space and are used to model various physical and abstract mathematical phenomena, from biology (DNA knotting) to physics (study of quantum fields).

"L8a8" is a notation from mathematical knot theory used to describe a specific type of link, which in this case, is a "link" that is topologically equivalent* (*meaning they can be transformed into each other without cutting or gluing) to a "seized carrick bend" knot commonly found in practical knot-tying.

In mathematics, particularly in knot theory, a link is a collection of knots that do not intersect but may be entangled with each other. A knot is essentially a loop in three-dimensional space that can be tangled but does not intersect itself.

Because knots and links can be transformed into each other without cutting or joining, they are essentially the same from a topological viewpoint. In other words, they have the same structure when considered in a mathematical sense.

This equivalence bridges abstract mathematics and practical applications. 

For instance, if the entire quipu knot system and mathematical manipulation with them was held in the minds of its users, could it suggest a technique that links or entangles conscious thought-forms with real-world applications? 

Perhaps this technique served as a kind of map, a guide for such intelligent agencies to be entangled together, to resonate and to manifest in our reality. 

Could this technique be applicable to various interactions with "the other side of reality," or might it represent an even deeper, more profound concept?

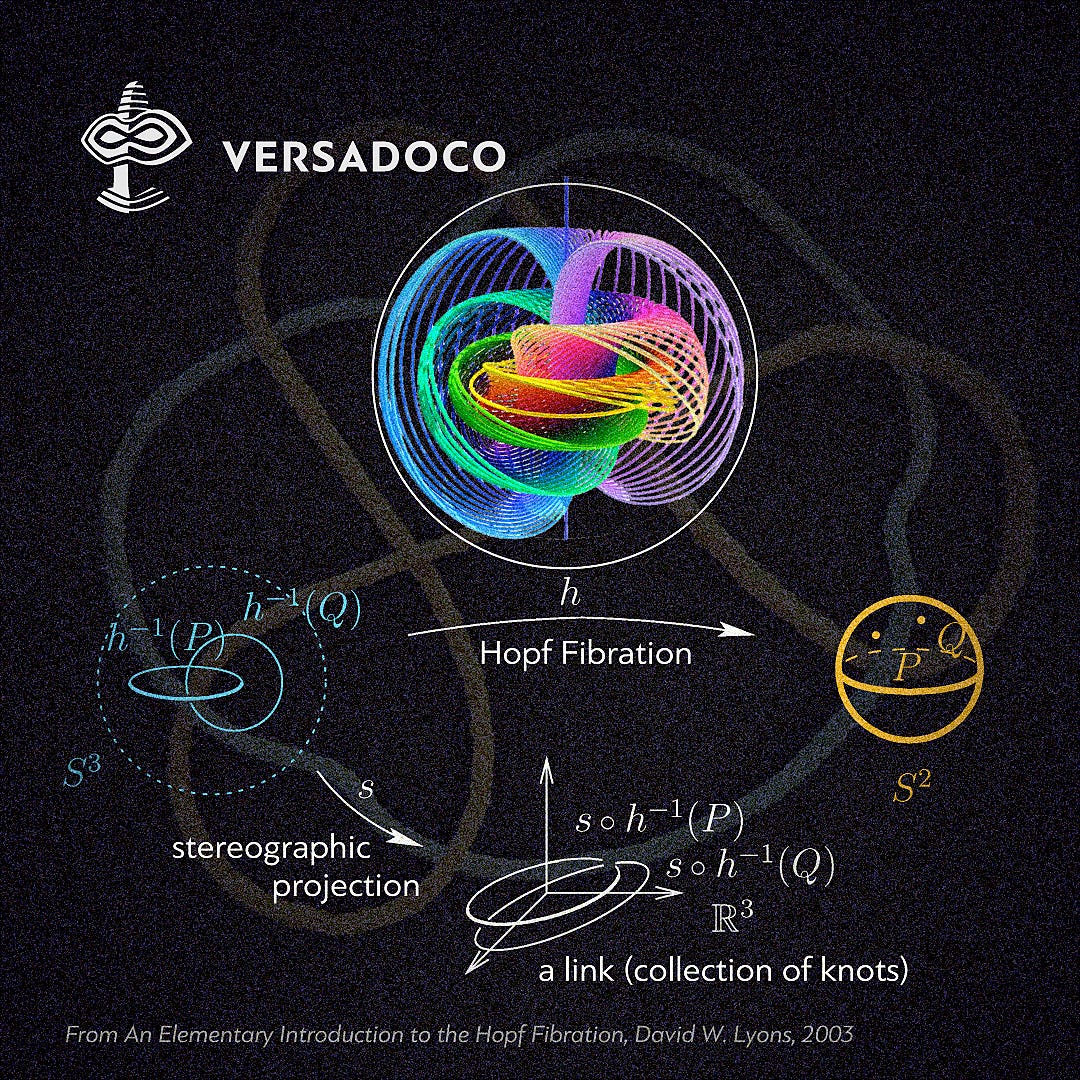
The idea isn't as fantastic as it might first appear. Consider that these seemingly abstract mathematical knots are directly connected to concepts in mathematical physics, condensed matter physics and photonics, such as the Hopf Fibration (explored in more detail in this episode -

The Hopf fibration is an extremely important concept and holds various implications. 

Historical accounts reveal that Heinz Hopf in topology and Paul Dirac in quantum physics discovered this structure concurrently, and in the same year. 

In the realm of physics, Dirac's discovery led to the concept known as the "Dirac monopole." It took decades for scientists to realize that these different concepts were manifestations of the same fundamental principle.

We discussed how magnetic structures akin to Dirac monopoles, can be useful in stone softening and transportation techniques in this episode -

Some scholars believe Hopf Fibration is crucial to grasping the holographic nature of the Universe, intertwining consciousness and matter.

In the words of the renowned mathematical physicist and Nobel laureate Sir Roger Penrose, the Hopf fibration can be considered as an "element of the architecture of our world." This concept is crucial in fields like quantum mechanics.

In the unique topological properties of the Hopf Fibration arises what physicists called Hopfions - "knots of stable energy" formed by the continuous twisting and interlinking within the Hopf Fibration framework.

These entities, shaped by knotting within the Hopf Fibration, maintain their stability due to their distinct configuration in space. In essence, Hopfions are like “lumps of energy knotted”, stable and self-sustaining, formed within the framework defined by the Hopf Fibration.

Hopfions are knotted vortices that exist within certain fields, like energy or magnetic fields. 

In photonic crystals and optical waveguides, Hopfions can be thought of as a kind of knot in the light flow and they can be described by a "linking number," which is a way of measuring how intertwined or linked these knots are, similar to how knots in a piece of string can be counted by how many times they loop around each other.

Let’s take these ideas a step further.

If Hopf Fibration is indeed a fundamental structure connecting consciousness and matter, then knowing how to manipulate this structure (that can be a process analogous to knotting in physical space) could theoretically alter the topology of reality itself.

"Topology of space" is a mathematical concept that describes the properties of a space that remain unchanged under continuous deformations, such as stretching or compressing, without tearing or gluing. It examines which shapes can be transformed into one another and which spatial structures remain invariant under such deformations.

In knot theory, connecting two ropes and creating knots alters the topology of the space in which these ropes exist. If this analogy extends to the Hopf Fibration and hopfions, it suggests that by "tying" or "altering" these topological structures, one could potentially modify the underlying fabric of reality.

This could imply a direct interaction between consciousness and the physical world, where changes in the topological structure (like creating a new knot) might have consequences in both realms.

If reality is fundamentally a topological structure like the Hopf Fibration, then the entire Universe could be viewed as a vast network of interconnected knots and links. Altering these (under special conditions, like changing the Gauge Symmetry) could lead to shifts in physical properties, the emergence of new physical phenomena, or even the way to manipulate consciousness.

In the context of quantum computing, knots and topological structures are explored as potential ways to create stable quantum bits (qubits). This connection between knot theory and quantum mechanics might hint at deeper links between the fabric of reality and information processing. 

If this idea is expanded to suggest that 'computers' are embedded in Nature or within matter itself and that there could be a way to access and manipulate their functions, the implications could be profound. More details in this episode -

If consciousness can be described using similar spatial properties, then interactions between different consciousnesses (or "minds", or “non-human intelligences”) might be akin to linking or knotting these topological structures. 

This perspective could lead to a new understanding of consciousness, where it is not just a product of the brain but also a fundamental spatial aspect of reality.

Could access to these "interfaces" have been achieved through visualization and the use of simple knot patterns, discovered and utilized by ancient people, but whose potential we have yet to fully realize?

A

Join this channel to get access to future perks  and support production:

https://www.youtube.com/channel/UCOJAGwgBflcY9EZHjpe0abw/join

🧢Versadoco Merch - https://versadoco-shop.fourthwall.com

⭐️Join us on Patreon https://www.patreon.com/_Versadoco_

Ways to Donate:

💸 PayPal donation - https://www.paypal.com/donate/?hosted_button_id=E9BVHT3PC5DEU

You can buy me a book from my wishlist here - https://www.amazon.com.au/hz/wishlist/ls/1N8WVKGSTHVLW?ref_=wl_share

Sources: 

https://en.wikipedia.org/wiki/Carrick_bend - Carrick bend knot

https://katlas.org/wiki/L8a8 - The Knot Atlas. L8a8 (mathematical "link" topologically equivalent to seized carrick bend of practical knot-tying).

https://kniganews.org/2013/06/17/beyond-clouds-731/ - Hopf Fibration and other ideas (original in Russian).

An Elementary Introduction to the Hopf Fibration, David W. Lyons - https://arxiv.org/abs/2212.01642 

Hopfion rings in a cubic chiral magnet -  https://www.nature.com/articles/s41586-023-06658-5 

Torus knots as Hopfions - https://www.researchgate.net/publication/236248539_Torus_knots_as_Hopfions 

Magnetic hopfions in solids - https://pubs.aip.org/aip/apm/article/10/11/111113/2835168/Magnetic-hopfions-in-solids