Узлы, Фибрация Хопфа и Хопфионы

Скрытая сторона узлов кипу?

Вот несколько дополнительных мыслей об узлах, которые мы обсуждали в документальном фильме о Кипу, здесь -

 Узел, изображённый на первом фото, также известен как «Плоский узел» и используется для соединения двух верёвок. Он особенно подходит для очень тяжёлых канатов или тросов, которые слишком большие и жёсткие для простого формирования других узлов. Этот узел не застревает, даже после значительных нагрузок или при намокании.

Интересно, что в теории узлов существует определённое математическое зацепление называемое L8a8, которое, при визуализации и манипуляциях в определённых условиях, напоминает морской «плоский узел», широко используемый на практике.

В математике теории узлов, зацепления представляют собой коллекции узлов, которые могут быть сложно переплетены, но не пересекаться (т.е. не проходить сквозь друг друга). Они существуют в трёхмерном пространстве и используются для моделирования различных физических и абстрактных математических явлений, начиная от биологии (узлы ДНК спиралей) до физики (изучение квантовых полей).

«L8a8» — это обозначение из теории узлов, используемое для описания конкретного типа зацепления, которое в данном случае представляет собой «связь», топологически эквивалентную* «плоскому узлу» 

(*означает, что объекты могут быть преобразованы друг в друга без разрезания или склеивания), который широко используется на практике.

Поскольку такие объекты, как узлы или связи, можно преобразовать друг в друга без разрезания или склеивания, они по сути одинаковы с точки зрения топологии. Проще говоря, у них одна и та же структура, если рассматривать её с математической точки зрения.

Эта эквивалентность создаёт мост между абстрактной математикой и практическими приложениями.

Например, если вся система узлов кипу (обсуждаемая в этом эпизоде — ссылка) и математические манипуляции с ними визуализировались её пользователями, заманчиво предположить, что это также обеспечивало особые условия, при которых используя определённые ментальные техники, шаманы были способны активно сцеплять или “заплетать в узлы”  образы мыслеформ с реальным физическим миром.

Возможно ли что такая техника служила своего рода шлюзом для энергии, некой визуализируемой направляющей для таких таких разумных сущностей, позволяя им сцепляться и резонировать и как следствие проявляться в нашей реальности? 

Применялась ли эта техника для взаимодействий с «другой стороной реальности» или же представляет собой некую более глубокую и более значимую концепцию?

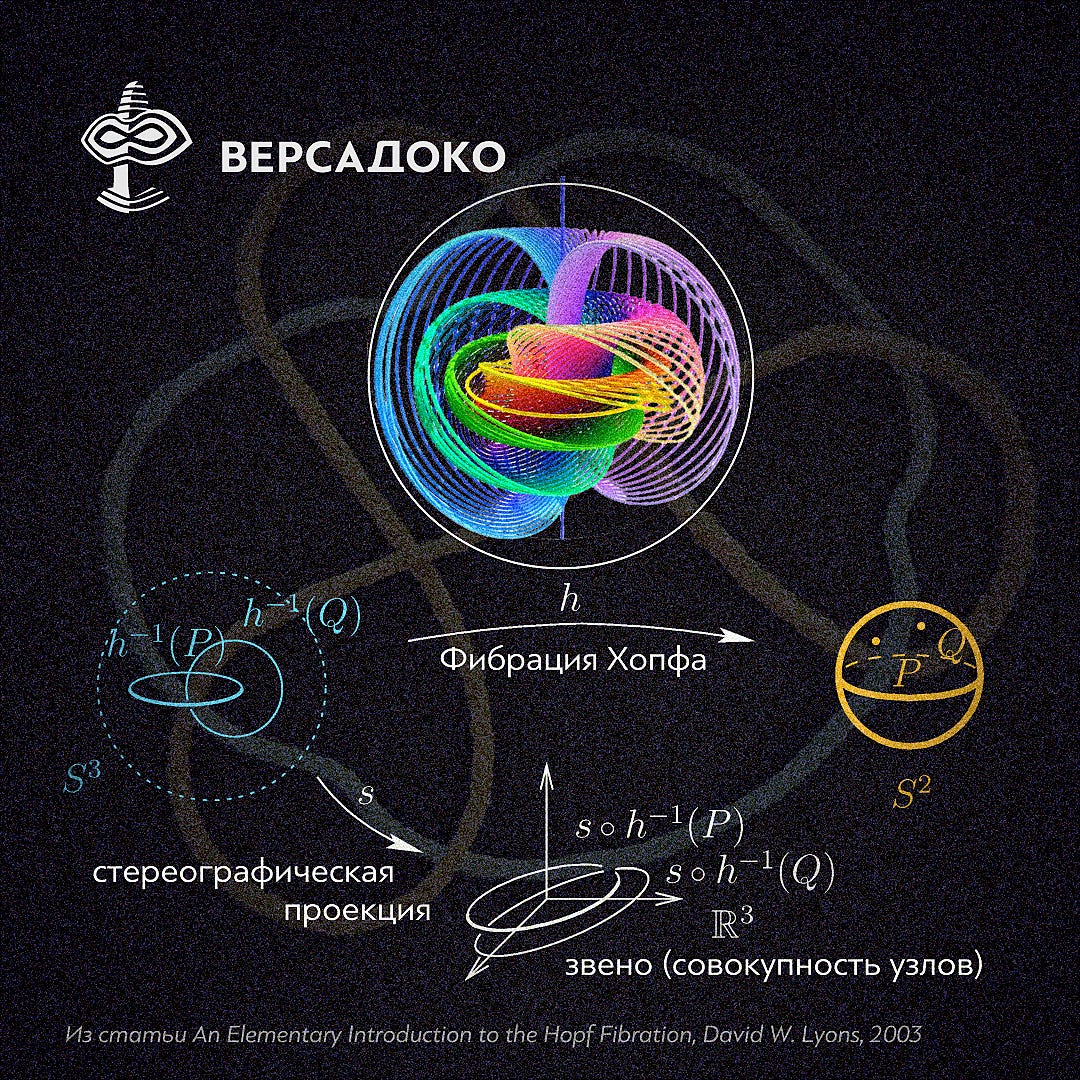
Эта идея не такая уж и фантастическая, как может показаться на первый взгляд, если учесть, что эти, казалось бы, абстрактные математические узлы уже напрямую связаны с концепциями в математической физике, физике конденсированных сред и фотонике, такими как Фибрация Хопфа (известна также как Расслоение Хопфа, подробнее рассмотрена в этом эпизоде —

Фибрация Хопфа — чрезвычайно важная концепция, которая имеет множество применений в науке. 

Исторические источники свидетельствуют о том, что Хайнц Хопф в области топологии и Поль Дирак в области квантовой физики открыли эту структуру одновременно и в одном и том же году. 

В области физики открытие Дирака привело к появлению концепции, известной как "монополь Дирака". Ученым потребовались десятилетия, чтобы понять, что эти разные концепции являются проявлениями одного и того же фундаментального принципа.

В этом эпизоде мы обсуждали, как магнитные структуры, похожие на монополи Дирака, могут быть полезны для размягчения камня и его транспортировки -

 Некоторые учёные считают, что эта структура является ключом к пониманию голографической природы Вселенной и обеспечивает связь между сознанием и материей.

По словам известного математика и физика, лауреата Нобелевской премии сэра Роджера Пенроуза, Фибрация Хопфа может считаться «элементом архитектуры нашего мира». Эта концепция также имеет ключевое значение в такой области, как квантовая механика.

В рамках Фибрации Хопфа и благодаря её уникальным топологическим свойствам в ней возникают так называемые хопфионы — «узлы стабильной энергии», сформированные непрерывным закручиванием и переплетением.

Эти объекты, существуют в виде переплетений и сохраняют свою стабильность благодаря своей особой конфигурации в пространстве. По сути, хопфионы похожи на «сгустки энергии, связанные в узлы», они очень стабильные и самоподдерживающиеся.

Другими словами, можно её сказать, что хопфионы — это вихри в виде узлов, которые существуют в определённых полях, таких как энергетические или магнитные поля. 

В фотонных кристаллах и оптических волноводах хопфион можно рассматривать как своего рода узел в потоке света, который может быть описан «числом связывания», которое представляет собой способ измерения того, насколько тесно переплетены или связаны эти узлы, подобно тому, как по виткам узлов на верёвке можно подсчитать, сколько раз они оборачиваются друг вокруг друга (представляя уже конкретное числовое значение, как в кипу).

Но можно поразмышлять и дальше…

Если Фибрация Хопфа действительно является фундаментальной структурой, соединяющей сознание и материю, то манипуляции с этой структурой — через процессы, аналогичные завязыванию узлов в физическом пространстве — теоретически могут изменять топологию самой реальности.

"Топология пространства" — это математическое понятие, которое описывает свойства пространства, которые сохраняются при непрерывных деформациях, таких как растяжение или сжатие, но без разрыва или склеивания, она рассматривает, какие формы могут быть преобразованы друг в друга и какие пространственные структуры остаются неизменными при деформациях.

В теории узлов соединение двух верёвок и создание узлов изменяет топологию пространства, в котором эти верёвки существуют. Если эта аналогия распространяется на Фибрацию Хопфа и хопфионы, это предполагает, что, «связывая» или «изменяя» эти пространственные структуры, можно потенциально влиять на саму ткань реальности.

Это может подразумевать как прямое взаимодействие между сознанием и физическим миром, где изменения в пространственной структуре (например, создание нового узла) могут иметь последствия в обеих сферах.

Если реальность фундаментально представляет собой топологическую структуру, подобную Фибрации Хопфа, то всю Вселенную можно рассматривать как обширную сеть взаимосцепленных узлов и связей. 

Изменение этих узлов (при особых условиях, например, изменении калибровочной симметрии) может приводить, к примеру, к изменениям физических свойств материалов, появлению новых физических явлений или даже к способам управления сознанием.

В контексте квантовых вычислений узлы и топологические структуры исследуются как потенциальные способы создания стабильных квантовых битов (кубитов). Такая связь между теорией узлов и квантовой механикой может намекать на более глубокие связи между структурой реальности и обработкой информации.

Если эту идею расширить, добавив, что “компьютеры” или “генераторы реальности” могут быть встроены в Природу или непосредственно в саму материю, и что существует способ доступа к ним и манипуляции их функциями, то последствия для практических приложений будут неотличимы от магии.

Детальнее в этом эпизоде —

Если сознание можно описать с использованием аналогичных пространственных свойств, то взаимодействия между различными сознаниями (или “разумами”, или “нечеловеческими интеллектами”) могут быть похожи на связывание или завязывание узлов в этих пространственных структурах. 

Это также может привести к новому пониманию сознания, где оно не просто продукт мозга, а фундаментальный пространственный аспект реальности.

Мог ли доступ к таким «интерфейсам» реальности быть получен путём визуализации и использования простых узловых паттернов, случайно (или неслучайно) обнаруженных и использовавшихся древними людьми, но потенциал которых мы уже сегодня совершенно не осознаём?

A

Станьте меценатом канала, чтобы ускорить выход новых видео:https://www.youtube.com/channel/UCOp58rDJcD-Tgfl8lmqtaKA/join

⭐️ На Boosty https://boosty.to/versadoco

⭐️ Отправить донат через Телеграм канал Версадоко - https://t.me/versadocorus

⭐️ Ежемесячная подписка через Телеграм канал Версадоко

🔹️1€ - https://t.me/tribute?start=s7397

🔹️1.83€ - https://t.me/tribute?start=s7396

🔹️2.44€ - https://t.me/tribute?start=s7398

🔹️3.66€ - https://t.me/tribute?start=s7399

🔹️18.32€ - https://t.me/tribute?start=s739a

🧢 Мерч Версадоко - https://versadoco-shop.fourthwall.com

💸 PayPal донат - https://www.paypal.com/donate/?hosted_button_id=E9BVHT3PC5DEU

Источники: 

https://ru.m.wikipedia.org/wiki/%D0%9F%D0%BB%D0%BE%D1%81%D0%BA%D0%B8%D0%B9_%D1%83%D0%B7%D0%B5%D0%BB - Плоский узел

https://katlas.org/wiki/L8a8 - The Knot Atlas. L8a8 (mathematical "link" topologically equivalent to seized carrick bend of practical knot-tying).

An Elementary Introduction to the Hopf Fibration, David W. Lyons - https://arxiv.org/abs/2212.01642 

https://kniganews.org/2013/06/17/beyond-clouds-731/ - Фибрация (Расслоение) Хопфа и другие интересные идеи, Книга Новостей, kiwi byrd 

Hopfion rings in a cubic chiral magnet -  https://www.nature.com/articles/s41586-023-06658-5 

Torus knots as Hopfions - https://www.researchgate.net/publication/236248539_Torus_knots_as_Hopfions 

Magnetic hopfions in solids - https://pubs.aip.org/aip/apm/article/10/11/111113/2835168/Magnetic-hopfions-in-solids